A non-mathematician’s view on the theory of electrical conductivity of aqueous solutions of strong electrolytes
Ivan Tikhonov
The article describes a method for calculating the specific electrical conductivity of an aqueous solution containing various types of ions. The influence of water on the principle of ion distribution in the volume of water is shown. The author explains why it is impossible to use the values of the equivalent electrical conductivity of individual ions to calculate aqueous solutions with different types of ions. Examples of calculating the specific electrical conductivity of aqueous solutions undergoing changes in ionic composition and the comparison of calculated and experimental data are given.
If we add sodium chloride (NaCl) to water, then this salt dissociates into the Na+ cation and the Cl– anion in water. Having received an electromagnetic field, this salt will be able to transfer an electric charge. In water, ionic conductivity will be observed, i.e. the electric charge will move due to the movement of Na and Cl ions.
According to the Debye-Hückel theory, it is assumed that a sphere of anions is formed around each cation in water and, accordingly, a sphere of cations is formed around each anion. Assuming that each ion can be represented as a point charge, the distribution of ions in water on the plane surface can be represented as follows. The ions form a hexagon at the vertices of which cations and anions alternate (figure 1). Then a sphere of equidistant anions is formed around each cation and vice versa. But it is true if we assume that it is a point charge.
In three dimensions, this structure will be depicted as a diamond crystal lattice, i.e. the carbon atom at the top of the hexagon will have four covalent bonds.
In this case, the atoms are equidistant from each other and at the same time, there is their mutual containment. They’re kind of jammed together. Perhaps for this reason, when atoms are arranged in the form of a hexagon, carbon, having the ability to build the same structures, determines organic life in all its diversity.
But what if there are divalent ions in the water and how to take into account different sizes of ions. For example, sulfate anions contain four oxygen atoms and one sulfur atom.
Nevertheless, it is believed that the Debye-Hückel-Onsager theory is quite applicable for calculating the values of the specific electrical conductivity of solutions for small concentrations.
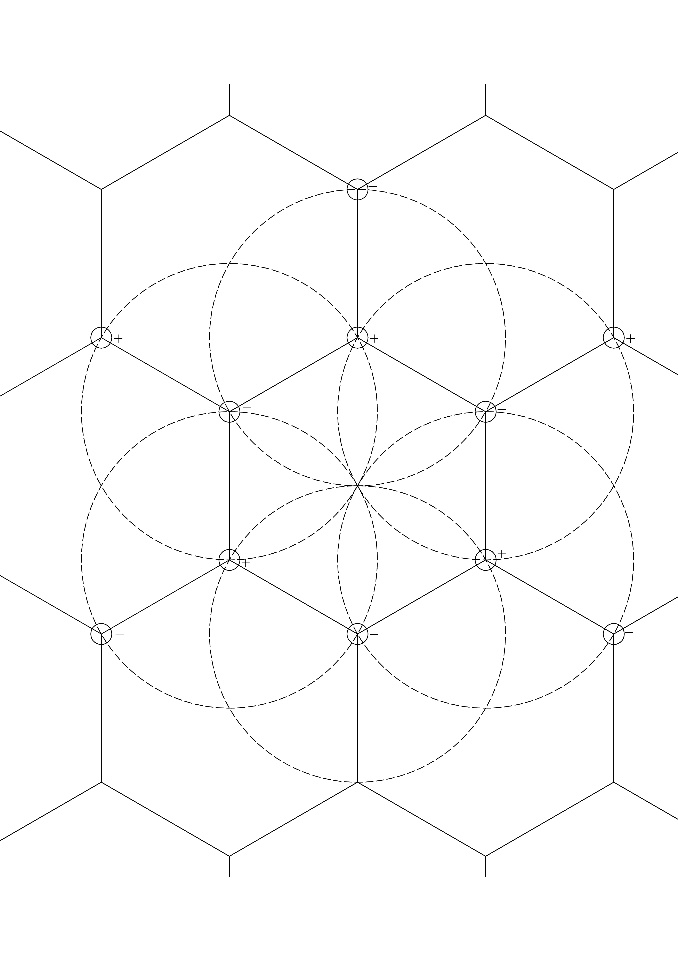
Figure 1
In accordance with this theory, in order to get away from the concept of point charge and come to ions, it is assumed that ions have a certain value of equivalent electrical conductivity at infinite dilution. In a physical sense, this means that if only a sodium cation is present in water and it is not affected by other ions, then this cation in an equivalent concentration can transfer a certain amount of electric charge. This assumption is in fact extremely controversial, because in water there cannot be only cations or anions. It is more correct to say that the possibilities for transferring the electric charge of cations are determined by its anion and vice versa.
In fact, the whole theory works only for electrolytes of valences 1-1, where ions with a certain assumption can be represented as a point charge.
Let’s look at an elementary example.
In my work, I am engaged in monitoring the water-chemical modes of boiler houses with various methods of water treatment. The most common method of water treatment is Na-cationic water softening. As a result of the search for means of remote control of such installations, it was found out that for fresh water, the electrical conductivity of softened water is almost always greater than the electrical conductivity of the original hard water. At the same time, the existing theory states the opposite.
The patent [1] uses the condition that the electrical conductivity of softened water is on average 5% greater than the electrical conductivity of the source water. This excludes scientific value, but makes this work a resource for discussion and subsequent identification of factors and patterns that determine this behavior of ions in an aqueous solution.
Indeed, as it will be shown later, for fresh calcium-magnesium-bicarbonate waters, on average, the electrical conductivity of softened water is on average 5% higher than the electrical conductivity of the original hard water. For water with a different ionic composition, the percentage of difference may vary significantly.
Let’s go back to the example.
There is the source water of the following ionic composition:
Cations (mg-eq/l): Ca=2,0; Mg=1,2; Na=0,78
Anions (mg-eq/l): HCO3=1,9; SO4=1,44; Cl=0,64
Total К=А=3,98 mg-eq/l
The measured electrical conductivity of this water was 409 µS/cm.
We calculate the electrical conductivity value using the electrical conductivity values of each ion depending on their total concentration in water. The dependence of the values of the electrical conductivity of ions on their concentrations is presented [2].
As a result, we obtain a value of electrical conductivity equaling 429 µS/cm.
Then we calculate the electrical conductivity of fully softened water. In this case, only sodium cations exist as cations. i.e., Na=3.98 mg-eq/l.
The calculated electrical conductivity of the softened water is equal to 418 µS/cm.
It turns out that the electrical conductivity of the source water is greater than the electrical conductivity of the softened water, which is incorrect.
In different sources, the dependence of the values of the electrical conductivity of ions on their concentration may differ slightly, but in general, this does not affect the calculation result. The electrical conductivity of the source water is always greater than the electrical conductivity of the softened water, which is not confirmed in practice.
This situation arises due to the fact that it is unacceptable to assume that an ion possesses only one certain value of equivalent electrical conductivity at infinite dilution, since this value will be different for ions of salts of valences 1-1 and 2-2.
How are the values of equivalent electrical conductivity obtained for infinite dilution?
Let’s consider two 1-1 salts: KCl and NaCl.
When dissociation occurs in water, the corresponding ions arise.
Then the assumption is made that if only cations of this salt existed in water, what the value of its electrical conductivity would be. And, accordingly, what would be the value of electrical conductivity if only anions existed in water. Then the average value of electrical conductivity is determined and divided by 2.
In order to implement this condition the concept of transfer numbers is introduced.
The transfer numbers indicate which share of the electric charge is transferred by the cation and, accordingly, how much by the anion.
i.е.
tk=λ0к/(λ0к+ λ0Cl) (1)
Where, t – transfer numbers of KCl
λ0к – equivalent electrical conductivity of potassium at infinite dilution.
λ0Cl – equivalent electrical conductivity of chloride at infinite dilution.
Accordingly
λ0Cl =1- λ0к
Likewise
tna=λ0na/(λ0na+ λ0Cl) (2)
Table 1 shows data on the equivalent electrical conductivity of calcium chloride and sodium at different mole concentrations (Cm*cm2* mol-1).
Table 1
| KCl | Λ0 | 0.5 mmol/l | 1 mmol/l | 5 mmol/l | 10 mmol/l | 50 mmol/l |
| K | 73,52 | 72,48 | 72,09 | 70,62 | 69,4 | 65,57 |
| Cl | 76,34 | 75,26 | 74,86 | 73,33 | 72,03 | 68,08 |
| Total | 147,75 | 146,95 | 143,95 | 141,4 | 133,65 | |
| NaCl | ||||||
| Na | 50,11 | 49,39 | 49,04 | 47,81 | 46,96 | 42,29 |
| Cl | 76,34 | 75,25 | 74,7 | 72,84 | 71,55 | 64,44 |
| Total | 124,65 | 123,74 | 120,65 | 118,51 | 106,74 |
The line “Total” indicates the equivalent electrical conductivity of the corresponding salt at the corresponding concentration. Thus, at a solution concentration of 1 mmol/l, the value of 146.95 for KCl and 123.74 for NaCl will be equal to the measured value in µS/cm. Accordingly, it is possible to obtain experimentally the values of equivalent electrical conductivities for both salts.
In Table 1, the second column immediately shows the result of interpolation to detect the values of the equivalent electrical conductivity of ions at infinite dilution.
Thus,
tk=λ0к/(λ0к+ λ0Cl) =73,52/(73,52+76,34)=0,49
tCl =1- λ0к=1-0,49=0,51
Thus potassium and chloride carry almost the same share of electric charges.
For a concentration of 0.5 mmol/l of KCl we have:
К=0,49*147,75=72,48
Сl=0,51*147,75=75,26
(the error in the calculations is due to the rounding to the second decimal place)
147,75 – the value obtained experimentally.
For NaCl
tna=λ0na/(λ0na+ λ0Cl)=50,11/(50,11+76,34)=0,396
tCl=1- tna =1- 0,396= 0,6
For a concentration of 0.5 mmol/l of NaCl we have:
Na = 0,396*124,65=49,39
Cl=0,6*124,65=75,25
Total= 49,39+75,25=124,65
It turns out that the value of the equivalent electrical conductivity of the NaCl solution at a concentration of 0.5 mmol/l, determined using the transfer numbers and initially set values of the equivalent electrical conductivity of ions at infinite dilution, is equal to the experimentally obtained value at this concentration.
The equality of the calculated values using the transfer numbers and the value of ions at infinite dilution and those obtained experimentally really confirms the possibility of using such a concept as the equivalent conductivity of an ion at infinite dilution.
But unfortunately, this concept only works for 1-1 electrolytes. In this case the assumptions made in the Debye-Hückel-Onsager theory are really largely fulfilled.
If we take a salt 2-1 or even more 2-2, then it is impossible to determine by selection, interpolation etc. a single value of the equivalent electrical conductivity of an ion at infinite dilution, which would be suitable for salts of different valence. For example, the value of the equivalent electrical conductivity of sulfate when infinitely dissolved in a compound with sodium (2-1) will differ significantly from the same value in a compound of sulfate and magnesium (2-2). This suggests that the value of the equivalent electrical conductivity of an individual ion at infinite dilution is not a basic physical quantity and cannot be used in the calculations of solutions with ions of different valence. In fact, this only finds application for calculations of salts 1-1.
That is why the calculation with the help of ions shows that softened natural water at low concentrations has a lower value of electrical conductivity than the original one. Which is incorrect. Since natural water contains various types of ions, including divalent ones, which makes it impossible to apply the concept of equivalent conductivity of an individual ion with infinite dilution.
It is necessary to say that the physical meaning has only the value of the equivalent electrical conductivity of the salt. Since the cation and anion are continuously connected and the properties of one depend on the properties of the other. At the same time, replacing the cation or anion in the pair the properties of the remaining ion also change. At least in the ability to transfer an electric charge. Which is caused by ion mobility. If the anion is less mobile, this is reflected in the cation. Although a direct dependence is not observed.
Let’s try to calculate the value of the electrical conductivity of an aqueous solution of ions of different valences knowing the experimental data on the equivalent electrical conductivity of salts.
The source water of our example contains 6 ions. Accordingly, 9 types of salts can be formed in water:
Ca(HCO3)2; CaCl2; Mg(HCO3)2; MgCl2; Na2SO4 – salts 2-1
СaSO4; MgSO4 – salts 2-2
NaHCO3; NaCl – salts 1-1.
The question arises, how to determine the concentration of each salt in water.
We can use the fact that the conductivity of all the studied finite volume of water is the same. I.e. if we take a small amount of water from the original finite volume, then the electroconductivity of these volumes of water will be the same. It can be concluded that the ions are distributed evenly in the volume of water, taking into account their valences.
Apparently, there is a principle that can be formulated as follows. The concentrations in mg-eq/l and the ratio of cation and anion concentrations in the initial volume of water are equal to the concentrations and the ratio of cation and anion concentrations in any separated (selected) smaller volume of water taken from the initial volume of water.
This principle of uniformity can be written as follows to determine the concentration of a particular salt (mg-eq/l):
![]() (3)
(3)
Where, Ск–а – concentration of the corresponding salt, mg-eq/l;
![]() – concentration of the corresponding cation, mg-eq/l;
– concentration of the corresponding cation, mg-eq/l;
![]() – concentration of the corresponding anion, mg-eq/l;
– concentration of the corresponding anion, mg-eq/l;
![]() – the sum of cations is equal to the sum of anions taken in mg-eq/l.
– the sum of cations is equal to the sum of anions taken in mg-eq/l.
Table 2 shows the calculation of the concentrations of salts found in the source water in accordance with the concentrations of ions.
That is, the total number of cations or anions is 3.98 mg-eq/l. In this case, the proportion of bicarbonate in the anionic part is 1.9/3.98=0.477.
Accordingly,
![]() = 2,0*1,9/3,98=2,0*0,477=0,955 mg-eq/l
= 2,0*1,9/3,98=2,0*0,477=0,955 mg-eq/l
Thus, the calculation is made for all 9 salts. The calculation is summarized in table 2.
Table 2
| Ions, mg–eq/l | HCO3=1.9 | SO4=1.44 | Cl=0.64 |
| Ca=2.0
0.955+0.724+0.322=2.0 |
2.0*(1.9/3.98)=
0.955 |
2.0*(1.44/3.98)=
0.724 |
2.0*(0.64/3.98)=
0.322 |
| Mg=1.2
0.573+0.434+0.193=1.2 |
1.2*(1.9/3.98)=
0.573 |
1.2*(1.44/3.98)=
0.434 |
1.2*(0.64/3.98)=
0.193 |
| Na=0.78
0.372+0.282+0.125=0.78 |
0.78*(1.9/3.98)=
0.372 |
0.78*(1.44/3.98)=
0.282 |
0.78*(0.64/3.98)=
0.125 |
| Sum:K=A=3.98 | 0.955+0.573+0.372
=1.9 |
0.724+0.434+0.282
=1.44 |
0.322+0.193+0.125=0.64 |
We get,
Ca(HCO3)2=0,955 mg-eq/l
CaSO4=0,724 mg-eq/l
СаCl2=0,322 mg-eq/l
Mg(HCO3)2=0,573 mg-eq/l
MgSO4=0,434 mg-eq/l
MgCl2=0,193 mg-eq/l
NaHCO3=0,372 mg-eq/l
Na2SO4=0,282 mg-eq/l
NaCl=0,125 mg-eq/l
As a result, at the beginning of the calculation, when we had only a chemical analysis of the concentration of individual ions, after applying the equation 3, we get the concentration values of all salts formed in water.
Now, using the method of transfer numbers, we can determine the value of the electrical conductivity of water based on the values of the electrical conductivity of individual salts (and not individual ions).
For this purpose, data from the source were used [3].
Since the calculation of the equivalent electrical conductivity of salts 2-2 is not possible according to the method proposed in [3], I conducted an experiment to determine the equivalent electrical conductivity for magnesium sulfate depending on the concentration. As a result, a more or less acceptable approximation of the obtained data was obtained only up to the range of 5 mmol/l of MgSO4 concentration. At higher concentrations, the calculation requires either a simple manual use of the data array, or probably a more complex approximation. Data for CaSO4 were taken assuming the behavior of calcium with respect to sulfate as in the compounds CaCl2 and MgCl2.
As a result, the equations of the dependence of the electrical conductivity values on the concentration for all 9 salts were obtained.
Next, the method of transfer numbers was used.
Electrical conductivity values were calculated for each of the 9 salts, provided that only this salt is contained in the water. The molar concentration of this salt corresponds to the molar concentration of all 9 salts.
Then the resulting concentration of each salt was multiplied by its actual molar concentration. As a result, the values of the electrical conductivity of each salt at its “real” concentration were obtained. Then these values are summed up and the value of the specific electrical conductivity of the aqueous solution is obtained.
The calculation results are presented in tables 3,4.
Table 3 shows the calculation of the total molar concentration of salts in the source water, as well as the calculation of the electrical conductivity of each salt and the calculation of the total electrical conductivity of the source water.
Table 4 shows the result of calculating the electrical conductivity of each salt depending on the total molar concentration of the aqueous solution.
Table 3
|
The source water
|
||||
| mmol/l | Cr, mg/l (ppm) | n | Er, µS/cm | |
| Ca(HCO3)2 | 0,477386935 | 77,33668 | 0,866096 | 89,29346 |
| СaSO4 | 0,361809045 | 49,20603 | 0,642424 | 76,59429 |
| CaCl2 | 0,16080402 | 17,84925 | 0,446322 | 39,99189 |
| Mg(HCO3)2 | 0,286432161 | 41,53266 | 0,80945 | 51,30972 |
| MgSO4 | 0,217085427 | 26,05025 | 0,581481 | 44,7998 |
| MgCl2 | 0,096482412 | 9,165829 | 0,400309 | 22,89686 |
| NaHCO3 | 0,372361809 | 31,27839 | 0,914854 | 34,1895 |
| Na2SO4 | 0,141105528 | 20,03698 | 0,58447 | 34,2823 |
| NaCl | 0,125427136 | 7,337487 | 0,477298 | 15,37297 |
| Total | 2,238894472 | 279,7936 | 0,684542 | 408,7308 |
Table 4
| mmol/l | mg/l (ppm) | n | µS/cm | |
| Ca(HCO3)2 | 2,238894472 | 362,7009 | 0,866096 | 418,7769 |
| СaSO4 | 2,238894472 | 304,4896 | 0,642424 | 473,9697 |
| CaCl2 | 2,238894472 | 248,5173 | 0,446322 | 556,812 |
| Mg(HCO3)2 | 2,238894472 | 324,6397 | 0,80945 | 401,062 |
| MgSO4 | 2,238894472 | 268,6673 | 0,581481 | 462,0395 |
| MgCl2 | 2,238894472 | 212,695 | 0,400309 | 531,3263 |
| NaHCO3 | 2,238894472 | 188,0671 | 0,914854 | 205,5707 |
| Na2SO4 | 2,238894472 | 317,923 | 0,58447 | 543,9506 |
| NaCl | 2,238894472 | 130,9753 | 0,477298 | 274,4101 |
At the beginning, the total molar concentration of salts in the water is determined (Table 3, second column). Then we assume that the water contains only one type of salt with total concentration and we calculate the value of the electrical conductivity of this salt at the total molar concentration of all salts (Table 4, column 5). The calculation uses experimentally obtained data for a specific type of salt. Then the conversion factor “n” is calculated.
n=C/E
Where, С – concentration of the corresponding salt in mg/l (ppm);
Е – Electrical conductivity of the same salt, µS/cm.
Then in table 3, the values in column 3 (Cr) are divided by the corresponding “n” values for each salt. The values of the electrical conductivity of each salt at its “real” concentration are obtained (Er).
Using this approach, the mutual influence of all ions on each other is taken into account.
As a result of the calculation, the measured value of the electrical conductivity of the source water of 409 µS/cm and the calculated value of 408.7 µS/cm practically coincided.
Table 5, 6 shows the calculation of the electrical conductivity of the same but fully softened water.
Only sodium is present as a cation in softened water. Accordingly in this water there are only three types of salt and please note that there are no salts 2-2.
As a result of the calculation, we obtain the electrical conductivity of softened water 423.58 µS/cm. The actual measured electrical conductivity of the softened water was 425 µS/cm.
Table 5
| The softened water | ||||
| mmol/l | Cr, mg/l (ppm) | n | Er, µS/cm | |
| NaHCO3 | 1,9 | 159,6 | 0,92321 | 172,875 |
| Na2SO4 | 0,72 | 102,24 | 0,591834 | 172,751 |
| NaCl | 0,64 | 37,44 | 0,480235 | 77,96177 |
| Total | 3,26 | 299,28 | 0,706536 | 423,5878 |
Table 6
| mmol/l | mg/l (ppm) | n | мкСм/см | |
| NaHCO3 | 3,26 | 273,84 | 0,92321 | 296,6171 |
| Na2SO4 | 3,26 | 462,92 | 0,591834 | 782,1782 |
| NaCl | 3,26 | 190,71 | 0,480235 | 397,1178 |
As it can be seen in this case, it is clearly traced that the softened water has a higher electrical conductivity than the original one.
It is obvious that the decisive effect on the increase in electrical conductivity is exerted by sulfate. The more sulfate in the source water, the higher the electrical conductivity of the softened water compared to the source water.
Quite a lot of experiments were carried out on mixing water with different concentrations of ions, and in general, the calculated values of electrical conductivity were quite close to the measured ones. In the range up to5 mmol/l of total salt concentration, the discrepancy between the measured and calculated values was no more than 3 µS/cm. Further, at high concentrations, the formation of ion pairs of salts 2-2 begins to affect results. Nevertheless, even at fairly high concentrations up to 50 mmol/l, there is a good convergence of the results.
Examples of the calculation program using the proposed method can be found in [4, 5].
A few words about the ion pairs in the 2-2 salts.
Ionic pairs in calcium and magnesium sulfate salts are easy to track if the electrical conductivity of softened water is continuously monitored. The fact is that at the beginning of the filter cycle, the softened water contains only sodium cation as a cation. After calcium or magnesium begins to slip into the softened water, the electrical conductivity of the water immediately drops sharply. The greater the slip of hardness ions, the smoother the line of dependence of electrical conductivity on the hardness of softened water becomes and eventually comes to a linear form, as predicted by the calculation program [6]. The fact is that small concentrations of calcium and magnesium are bound by sulfate into ion pairs and cease to carry an electric charge. Because of this, there is a sharp drop in electrical conductivity, since the equivalent amount of sodium, that was previously in the softened water, transferred the charge because sodium was not bound into an ion pair. Thus, at a sulfate concentration of about 40 mg/l, the drop in electrical conductivity was about 3 µS/cm (with total concentration of calcium and magnesium of 2.8 mg-eq/l). At sulfate concentration of 90 mg/l, the drop was about 5 µS/cm (with total concentration of calcium and magnesium of 3.3 mg-eq/l). I.e., in the first case, the ion pair was 0.011 mmol/l or 1.5 mg/l CaSO4 if we count calcium. In the second case, 0.018 mmol/l or 2.45 mg/l CaSO4.
Therefore, when the equivalent electrical conductivities of salt 2-2 is determined experimentally it is necessary to understand the presence of an error caused by the ion pairs of this salt.
In salts 2-1, it is likely that if ion pairs are formed, then it is observed in very small quantities. Because when the hydrogen ion is replaced with sodium ions in water with sulfates, the dependence of electrical conductivity on the sodium concentration has a linear form. Probably, ion pairs in salts 2-1 can be neglected at least at concentrations up to 10 mmol/l.
In conclusion.
This paper primarily discusses the validity of using such a concept as the principle of uniform distribution of ions in the volume of water. This principle (if it can be called so) does not come naturally from the concept of electroneutrality of solutions. The use of this principle allows, at least at low concentrations for strong electrolytes of various types of ions to produce a fairly accurate calculations of the values for conductivity of aqueous solutions. This will help to avoid the usage of the concept of equivalent conductivity of the individual ion at infinite dilution. Is this principle universal or is it a special case in this example?
With respect,
Ivan Tikhonov
References
- DOPSLAFF HARTMUT; DOPSLAFF CARSTEN H + «Blending control method with determination of untreated water hardness via the conductivity of the soft water and blended water», Application number NZ20130720562 20131217
- Ivan Tikhonov, The influence of ion composition of water on its electrical conductivity – https://tiwater.info/en/the-influence-of-ion-composition-of-water-on-its-electrical-conductivity/
- Methodological guidelines for the use of conductometric control for maintaining the water modes of power plants МУ 34-70-114-85 (РД 34-37-302)
- Ivan Tikhonov, Changes in the electrical conductivity of natural water when adding hydrochloric and sulfuric acid to it – https://tiwater.info/en/changes-in-the-electrical-conductivity-of-natural-water-when-adding-hydrochloric-and-sulfuric-acid-to-it/
- Ivan Tikhonov, The control of the process of acid ion exchange of water using the value of the specific electrical conductivity of water – https://tiwater.info/en/the-control-of-the-process-of-acid-ion-exchange-of-water-using-the-value-of-the-specific-electrical-conductivity-of-water/
- Ivan Tikhonov, The method of controlling the process of ion exchange water softening – https://tiwater.info/en/the-method-of-controlling-the-process-of-ion-exchange-water-softening/

